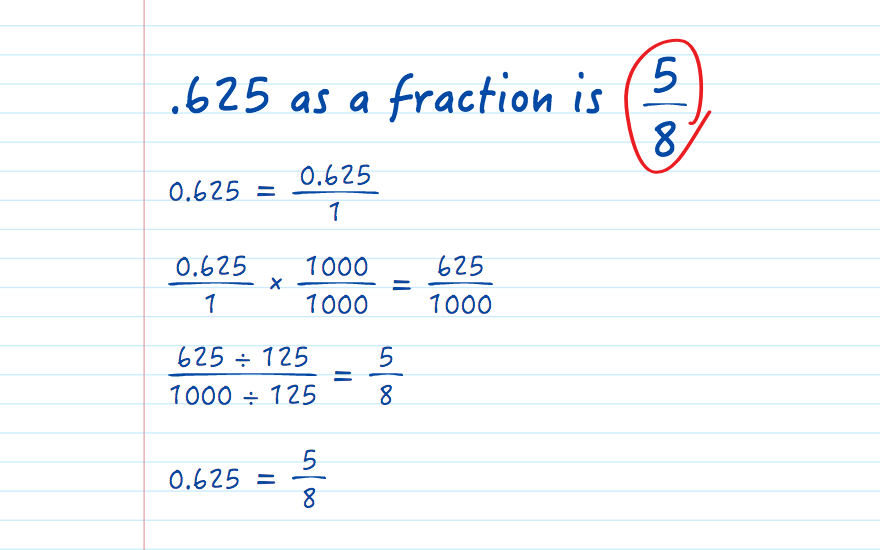625 As A Fraction
Can a seemingly simple decimal like 0.625 truly unlock a deeper understanding of mathematical principles? The answer, surprisingly, is a resounding yes. The ability to convert decimals to fractions is a fundamental skill that underpins a wide range of mathematical concepts and real-world applications.
The conversion of decimals to fractions, while appearing elementary, is a gateway to grasping the relationship between different numerical representations. It allows us to move seamlessly between the world of whole numbers and the realm of parts of a whole, enriching our comprehension of quantity and proportion. But how, precisely, do we bridge this gap? Let's delve into the specifics, armed with the knowledge that the seemingly humble decimal 0.625 holds the key.
| Concept | Converting Decimals to Fractions |
| Starting Point | The decimal number 0.625 |
| Core Principle | Understanding place value and the relationship between decimals and fractions |
| Initial Conversion | 0. 625 / 1 |
| Step 1: Numerator and Denominator | Write the decimal as a fraction over 1: 0.625/1 |
| Step 2: Eliminate the Decimal | Multiply the numerator and denominator by a power of 10 (10, 100, 1000, etc.) to eliminate the decimal point. Since 0.625 has three decimal places, we multiply by 1000: (0.625 1000) / (1 1000) = 625/1000 |
| Step 3: Simplify (Reduce) | Find the Greatest Common Divisor (GCD) of the numerator and denominator. The GCD of 625 and 1000 is 125. |
| Step 4: Divide by GCD | Divide both the numerator and denominator by the GCD: 625 / 125 = 5, 1000 / 125 = 8. |
| Final Result | The simplified fraction is 5/8. |
| Simplified Fraction | 5/8 |
| Equivalent Representation | 0. 625 = 5/8 |
| Verification | Divide 5 by 8 using a calculator; the result should be 0.625. |
| Reference Website | MathsIsFun |
The transformation begins by recognizing 0.625 as a part of a whole. It is a decimal, and to convert it into a fraction, we need to understand its place value. The digits to the right of the decimal point represent fractions of a whole number. The "6" is in the tenths place, the "2" is in the hundredths place, and the "5" is in the thousandths place. This immediately suggests a connection to fractions with denominators of 10, 100, or 1000.
The first step is to express 0.625 as a fraction over 1: 0.625/1. This is simply a way of framing the decimal within a fractional context. The real work starts when we want to eliminate the decimal point. Because 0.625 has three digits after the decimal point, we can get rid of the decimal by multiplying both the numerator and denominator by 1000 (10 to the power of 3). This gives us: (0.625 1000) / (1 1000) = 625/1000.
Now, we have a fraction, but it's not in its simplest form. To get the simplest form, we need to reduce the fraction. This means finding the greatest common divisor (GCD) of the numerator (625) and the denominator (1000). The GCD is the largest number that divides both numbers without leaving a remainder. In the case of 625 and 1000, the GCD is 125.
Finally, we divide both the numerator and the denominator by the GCD (125). This gives us 625 / 125 = 5 and 1000 / 125 = 8. The simplified fraction, then, is 5/8. This is the simplest form of the fraction that represents the original decimal, 0.625.
Let's revisit the steps to convert the decimal into a fraction, step-by-step: Starting with the decimal, 0.625. Write the decimal over 1 to have the fraction structure. To convert the decimal, we can represent it as 0.625/1. As we know, 0.625 has three digits after the decimal point. As a result, we will multiply both numerator and denominator by 1000. 0.625 x 1000 = 625 and 1 x 1000 = 1000. 625/1000, is the initial fraction value.
Once we've transformed the decimal into a fraction, the next task is simplification. The fraction 625/1000 can be simplified. Simplify the fraction by dividing both the numerator and the denominator by their greatest common factor. The Greatest Common Divisor (GCD) of 625 and 1000 is 125. 625 / 125 = 5 and 1000 / 125 = 8.
So, the simplified fraction becomes 5/8. This is the simplest fraction form of the decimal 0.625.
This method works because multiplying by 1000 (or any power of 10) shifts the decimal point three places to the right, effectively turning the decimal into a whole number. The denominator reflects the original place value of the decimal the thousandths place in this instance. Furthermore, dividing by the GCD is essential; this ensures the resulting fraction is expressed with the smallest possible numbers, making it easier to understand and work with. The process is the same for any decimal. Count the numbers after the decimal point and multiply numerator and denominator by that power of 10. Find the GCD of the numerator and denominator and simplify.
The concept extends beyond just 0.625. For example, consider the decimal 2.695. To convert this into a fraction, you would follow a similar process. First, recognize that you have whole units (the "2" before the decimal point). Focus on the decimal portion (.695). Since there are three digits after the decimal point, you'd multiply both the numerator and denominator by 1000, resulting in 695/1000. Simplify this fraction to its simplest form (in this case, the GCD is 5, leading to 139/200). Finally, combine the whole number and the simplified fraction: 2 139/200. This is equivalent to the decimal 2.695.
This process of converting decimals to fractions is not just an academic exercise. It is a fundamental skill with wide-ranging practical applications. Recipes, for instance, frequently call for fractional measurements. Understanding how to convert decimals like 0.625 (which is 5/8) is critical for accurately scaling recipes up or down. Similarly, in construction and engineering, where precise measurements are paramount, the ability to seamlessly move between decimal and fractional representations is a necessity.
When confronted with a measurement of 2.695 inches, it can be useful to convert the decimal portion to a fraction. To start, as we know, we can represent the decimal portion as the fraction 695/1000. But this is not the simplest form, so, we reduce it. In this case, the greatest common divisor (GCD) of 695 and 1000 is 5. If we divide both the numerator and the denominator by 5, we get 139/200. Note that we use an "approximately equal" sign to demonstrate the difference, because we have to round the fractional values to their closest form. Now, we can convert the fraction 139/200 to a fraction over 16 by doing the math to calculate the missing value. As such, 139/200 is approximately 11/16. When we use this method, we can see that 2.695 decimal inches are approximately equal to 2 11/16 as an inch fraction.
Moreover, understanding how to manipulate fractions and decimals underpins more advanced mathematical concepts, such as ratios, proportions, and percentages. For example, the percentage 1.3% can be understood as the fraction 1.3/100. This can be further converted to a fraction. Multiply the numerator and denominator by 10. 1.3 x 10 = 13 and 100 x 10 = 1000. 1.3% is also equivalent to the fraction 13/1000.
The ability to convert between decimals and fractions enhances numerical literacy. It empowers individuals to interpret, manipulate, and apply numbers in various contexts, making them more confident problem-solvers. Whether it's calculating the dimensions of a piece of furniture, adjusting a recipe, or understanding financial statements, a solid grasp of decimal-to-fraction conversions provides the foundational skills.
In essence, converting a decimal to a fraction simplifies the process to its most fundamental parts. Take the decimal, put it over one, then multiply both the numerator and the denominator by the required value to remove the decimal. Finally, simplify the fraction by reducing it. 0.625, as demonstrated, is a classic illustration, it becomes 625/1000, which simplifies to 5/8.
To reiterate, to convert 0.625 to a fraction, one can write it over 1, multiply the numerator and denominator by 1000, and reduce to get the final answer of 5/8. 5/8 is the simplest fractional form of the decimal 0.625. The fractional representation can easily be confirmed by the division of 5 by 8. The result of the division will be equal to the decimal, 0.625.
What's more, let's convert 1.3 to a fraction. Following the same rule, we write the number as a fraction. 1.3 becomes 1.3/1. As we know, 1.3 has one digit after the decimal point, so, we multiply the numerator and denominator by 10. 1.3 x 10 = 13 and 1 x 10 = 10. 1.3 can also be written as 13/10. Now, by simplifying, we get 13/10 = 1 3/10 as a fraction.
The significance of converting decimals to fractions extends into fields far beyond basic arithmetic. In cooking, it makes the difference between success and failure. Knowing that 0.625 of a cup is the same as 5/8 of a cup allows the accurate measuring of ingredients. In carpentry and other trades, the ability to convert decimals to fractions is essential for making precise measurements. This also applies to those working with different systems of measurement, like metric versus imperial, where this skill can be invaluable.
This process might seem simple. However, it can be a powerful method. 0.625 is 5/8. Converting 0.625 is not complicated at all. The process is fundamental, the steps are easy, and the application has far reaching impacts. The concept is very straightforward; the utility is remarkably broad.
In conclusion, while the journey to convert a decimal into its fractional counterpart may seem like a straightforward mathematical operation, its importance lies in its ability to enhance mathematical literacy. The conversion of decimals to fractions, as demonstrated by the example of 0.625, provides a gateway to understanding place value, the relationships between whole numbers and parts, and the power of simplifying complex numerical structures.