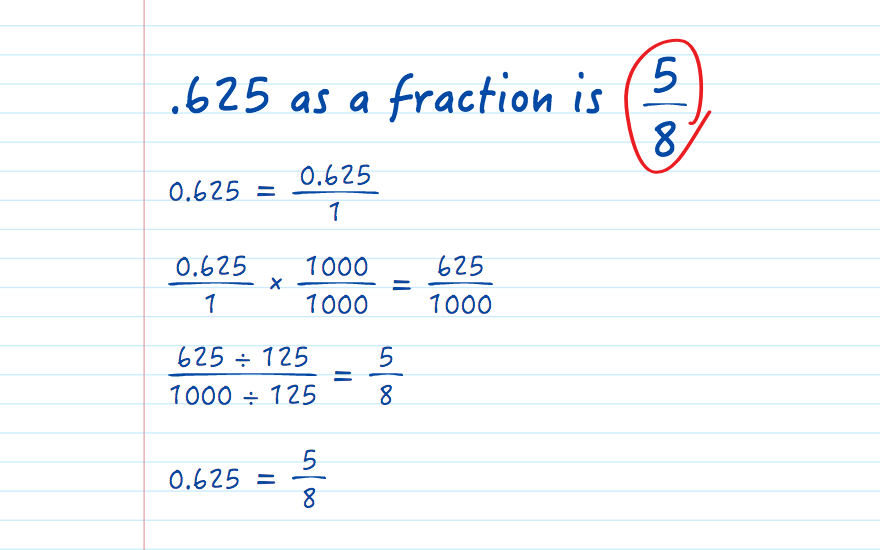Convert Decimals To Fractions: Step-by-Step Guide
Ever struggled with converting a decimal into a fraction, feeling lost in a sea of numbers? Converting decimals to fractions is a fundamental skill, and understanding this process unlocks a clearer understanding of mathematical concepts and real-world applications.
The ability to seamlessly switch between decimal and fractional forms is a surprisingly useful skill, applicable in numerous areas from cooking and carpentry to finance and scientific calculations. This article delves into the straightforward process of converting decimals to fractions, focusing specifically on the often-encountered decimal, 0.625. We'll dissect each step, providing clear examples and explanations to make the conversion process simple and easy to understand.
Before we proceed further, let us delve into some relevant data and information.
| Aspect | Details |
|---|---|
| Decimal Value | 0.625 |
| Equivalent Fraction | 5/8 |
| Decimal Places | 3 |
| Representation | 625 thousandths |
| Simplification Method | Finding the Greatest Common Divisor (GCD) |
| GCD of 625 and 1000 | 125 |
| Applications | Recipes, measurements, financial calculations |
| Related Concepts | Place value, equivalent fractions, simplifying fractions |
| Example | 2.695 = 2 11/16 |
For Further Reading and Verification, Refer to Math Is Fun for more information and insight.
Let's start with the basics: what exactly does a decimal represent? A decimal is a number that represents a value that is less than a whole number. It uses a decimal point (.) to separate the whole number part from the fractional part. For instance, in the decimal 0.625, the '0' represents the whole number (in this case, zero whole units), and '.625' represents the fractional part. To understand this further, consider the place value of each digit after the decimal point.
In the decimal 0.625, the '6' is in the tenths place, the '2' is in the hundredths place, and the '5' is in the thousandths place. This means 0.625 can be read as "six hundred and twenty-five thousandths." This is the key to converting the decimal to a fraction: understanding that the last digit's place value determines the denominator of the fraction. In the case of 0.625, the '5' is in the thousandths place, thus the fraction initially is written as 625/1000.
So, how do we take the decimal 0.625 and convert it into its fractional form? The process is remarkably straightforward. First, write the decimal as a fraction over one. In other words, 0.625 becomes 0.625/1. While this might seem like an unnecessary step, it sets the stage for the next part: removing the decimal point.
To remove the decimal point from the numerator, we will multiply both the numerator and the denominator by a power of 10. The power of 10 is determined by the number of digits after the decimal point. Since 0.625 has three digits after the decimal point (6, 2, and 5), we will multiply both the numerator and the denominator by 103, or 1000. This gives us:
(0.625 1000) / (1 1000) = 625 / 1000
Now we have the fraction 625/1000, which is equivalent to the decimal 0.625. But, this is not yet in its simplest form. To get the simplest form of the fraction, we need to reduce or simplify it.
Simplifying a fraction involves dividing both the numerator and the denominator by their greatest common divisor (GCD). The GCD is the largest number that divides evenly into both the numerator and the denominator. In the case of 625/1000, the GCD of 625 and 1000 is 125.
Dividing both the numerator and the denominator by 125, we get:
(625 125) / (1000 125) = 5 / 8
Therefore, the simplest fraction form of 0.625 is 5/8. The decimal 0.625 is thus represented as five eighths.
Let us recap the conversion process from the very beginning, to convert 0.625 to a fraction, we follow these steps:
- Write the decimal as a fraction over 1: 0.625/1
- Multiply the numerator and denominator by a power of 10 to eliminate the decimal (in this case, 1000): (0.625 1000) / (1 1000) = 625/1000
- Simplify the fraction by dividing the numerator and denominator by their GCD (125): (625 125) / (1000 125) = 5/8
This method is universally applicable. For example, if you wanted to convert 1.3 to a fraction, you'd write it as 1.3/1. Then multiply the top and bottom by 10 (since there is one digit after the decimal) to get 13/10. Finally, convert this improper fraction to a mixed number, resulting in 1 3/10. The key is consistently applying the steps, and understanding what the decimal digits represent within a fractional context.
Consider another example with a slightly more complex number, let's say 2.625. To convert this, first write it as a fraction over 1, 2.625/1. Then multiply the numerator and denominator by 1000 (since there are three digits after the decimal) to remove the decimal point. Thus we obtain 2625/1000. Finally, simplify the fraction by dividing both numerator and denominator by their GCD, which is 125. This simplifies to 21/8. Convert to a mixed number, 2 5/8.
When working with decimals, it is essential to recognize place value; that's tenths, hundredths, thousandths, and so on. A deep understanding of place value facilitates seamless transitions from decimal form to fractional form, and back again. This fundamental knowledge enables you to rewrite any decimal number as a fraction, whether it be a simple 0.5 or a more intricate 3.785.
The process of decimal-to-fraction conversion is also incredibly useful in practical contexts. Recipes often require precise measurements, and knowing that 0.625 is the same as 5/8 can be incredibly helpful when adjusting ingredient amounts. Similarly, carpenters, and anyone else dealing with measurements, often encounter decimal inches (or other measurement units), quickly converting them into fractions, providing accuracy, and precision in their work.
Converting decimals to fractions is not just an exercise in mathematical manipulation; it is a gateway to a deeper understanding of numbers and their relationships. The ability to switch between these representations enhances a person's numerical literacy and provides the tools needed to solve mathematical problems. Mastering this conversion also lays the foundation for more advanced mathematical concepts.
In summary, the conversion of 0.625 to a fraction follows these critical steps:
- Acknowledge the place value of the last digit (thousandths).
- Represent the decimal as 625/1000.
- Reduce the fraction to its simplest form using the GCD, resulting in 5/8.
This methodical approach ensures that the decimal is accurately converted into a fraction, allowing for easier mathematical operations, better interpretations, and accurate application in real-world scenarios. Remember that decimals represent fractions, and understanding this relationship will strengthen your mathematical skills.